i207M's Fantastic Blog

Welcome

0%

离散数学(2)课程小记

发表于 分类于

学习离散数学(2)过程中的一些记录。

图论

道路与回路

简单道路：边不重复

初级道路：点不重复

1
2
3
4
5
回路：起点终点相同
简单通路：起点到终点所经过的边不同
简单回路：起点到终点所经过的边不同+回路
初级通路：起点到终点所经过的顶点各异+简单通路
初级回路/圈：起点到终点所经过的顶点除起点终点相同外，其余顶点各异+简单回路

如果简单图G的任意两结点之间恒有，则G中存在哈密顿回路。

如果简单图G的任意两结点之间恒有，则G中存在哈密顿道路。

此定理的证明妙啊！

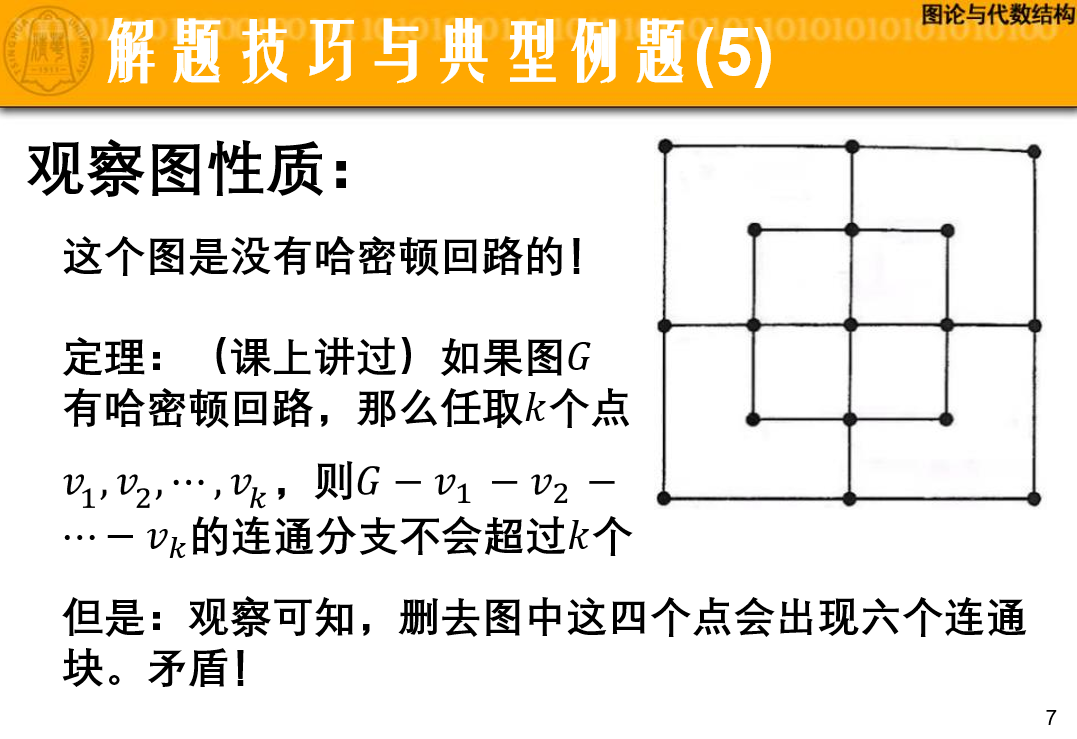
如果图G有哈密顿回路，那么任取k个点，则的连通分支不会超过k个。

哈密顿回路问题可转化到闭合图上。

有关道路、回路的题目的证明技巧：以最长初级道路为基础。

在满足三角不等式的前提下，TSP问题的便宜算法得出的近似解与实际最优解之比.

邮递员问题（中国邮路问题）的充分必要条件的证明也很妙啊！

  • G的每条边最多重复1次
  • G的任一回路上重复边的长度之和不超过该回路长度的一半

树

基本关联矩阵：关联矩阵去掉一行。

生成树计数的矩阵的结果就是基尔霍夫矩阵.

必经某边的（有向）生成树计数：将的其他入边删除；或原答案-删边后的答案。

回路矩阵

完全回路矩阵：

  • . 证明从两个方向。
  • . 证明方法：对回路与点的相关性进行分析。

基本回路矩阵：回路仅含一条非树边，可以写为.

  • （其中）. 感觉很神奇，我还不太理解逆矩阵的几何意义。

割集矩阵

割集：要求“最小”。

完全割集矩阵：

基本割集：

image-20210330114547686

基本割集矩阵：仅含一条树边，可以写为

  • . 这更神奇了。

无法直观理解…

平面图

平面图：，分别为域、连通块数量。

因为没有割边，所以每条边都与两个不同的域相邻。域边界数对域求和等于2m.

简单平面图，一定存在度数的节点。

极大平面图.

若简单图G不含子图，则有.

的极大平面图，每个点的度数大于等于3.

若，则G可平面。

判定图的平面性：先按连通块、割点拆开。然后循环：去掉度为2的点，去掉重边。

若G是平面连通图，则.

G有对偶图等价于G为平面图。

平面图的对偶图是平面图。

image-20210412192445421

image-20210413103111065

图的着色

非空图的色数=2当且仅当没有奇回路。

平面连通图的域可以2着色当且仅当G中存在欧拉回路。

必要性：

无奇回路 -> 域边界数为偶数 -> 再对偶，原图点度为偶数 -> 有欧拉回路

充分性同理。

点2着色当且仅当连通图G有欧拉回路。

习题课对知识的讲解不错

匹配与网络流、图的连通性：鸽了

补一个最佳匹配算法：

  1. 每行每列有一个界值，初始时每行的界值为本行最大值，每列的界值为0，行列界值之和将会是答案

  2. 构造矩阵B，

  3. 对0进行最小覆盖，直到覆盖数=n

  4. 否则，在未覆盖元素中选择最小非零元a，把a调成0。（也就是若i行j列已覆盖，+a；）若i行j列未覆盖，-a

    修改界值，行取最大值，也就是没覆盖的行-a；已覆盖的列+a

  5. 于是重新求最小覆盖

代数结构

概念

代数系统：集合+若干运算

半群：集合+一个二元运算满足结合律

(含)幺(半)群：半群+单位元=结合律+单位元

交换幺群：幺群+交换律

循环幺群：幺群，且

群：所有元素都可逆的含幺半群=结合律+单位元+可逆

交换群、阿贝尔群：满足交换律的群

阶：群G中元素a，O<a>，称为a的阶或周期。群的阶数是元素的个数。

循环群：群，且

定理

半群（幺群）的满同态也是半群（幺群）。

设G=<a>, O<a>=n，则G有个生成元；若O<a>=，则生成元只有。

循环群的子群也是循环群。若还是无限群，则子群也是无限群；若有限群，则。

n阶循环群和同构。

Cayley定理：任意群G和一个变换群同构。

Lagrange定理：设G是有限群，H是G的子群，则

以下是复习时写的：

复习

经典结论

6个人中如果没有3个人互相认识，则至少有3个人相互不认识。

点的度数和为偶数。

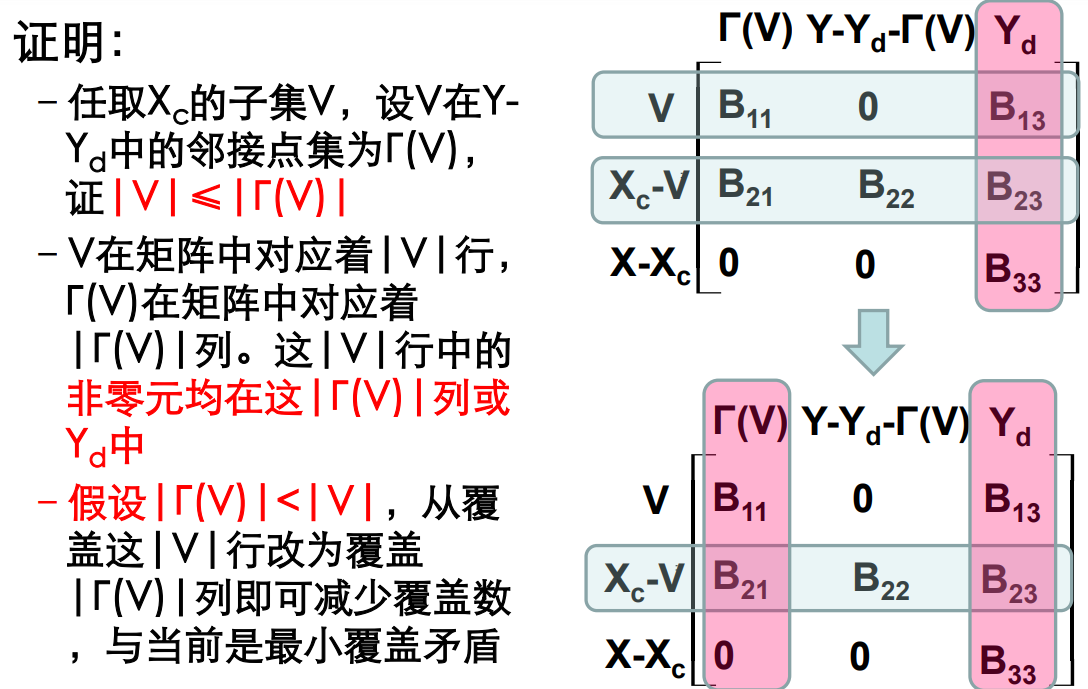
Hall定理：完全匹配的充要条件$\forall A\subset X,|\Gamma(A)|\ge |A| $.

image-20210614101145370

image-20210614100454334

二分图的最大匹配数r，与其邻接矩阵的最小覆盖数s相等。

无割点的等价性质：

image-20210614212644991

证明技巧

度数对边求和，得到的是度数的平方。

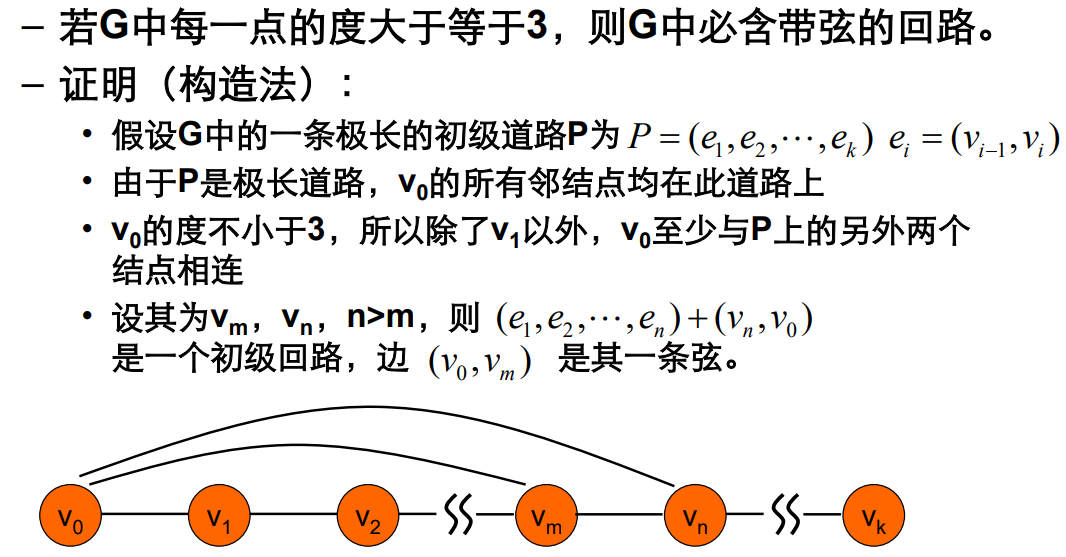
极长道路的端点的出边都在道路上。

构造性的证明。先假设存在小回路，然后每次扩展一个点。

哈密顿回路相关

  • 的连通分支不超过|S|个
  • 闭合图
  • 证明没有H回路：
    • 二分图黑白点个数相同
    • 存在H回路上相邻的点，两点都和A相连

拼不等式，通过某项把两个方向的不等式连起来。

每两个面之间最多一条公共边每个点度数.

构造集合。

H是G的子群的充要条件是：对于任意的.

启发性的证明

image-20210612104635519

image-20210612111701535

image-20210612163026019

image-20210612231540202

五色猜想

image-20210615155353502

image-20210614101002418

设简单连通图G的节点数是15,其中8个点的度是4，6个点的度是6，一个点的度是8，证明：G是非平面图。

证明：因为每个结点的度都是偶数。所以存在欧拉回路。所以G的域可以2着色。

极大平面图的域都是三角形，而且满足m=3n-6. 由计算可知，G的边数比极大平面图正好少了1. 也即，G中除了一个域的边数是4，其余的边数是3. 即，除了一个域的边数不能被3整除，其余均可被3整除。所以G的域不可2着色。推出矛盾。

若无割边的平面图除一个域外，其余各域的边界数都可以被整除，则G的域不可被二着色。

证明：从度数奇偶性入手。

image-20210614101427714

image-20210614194146863

image-20210614194316820

image-20210614234340904