习题二
8.
设 G 是的简单图,证明:若
,则 G 存在 H 回路。
数学归纳法。当时,命题显然成立。
假设时命题成立,现证明
时成立。
Lemma 1:.
化简,得,移项得
,故证毕。
Lemma 2:G 中度数最大的点的度数.
由知,
.
反证法。假设所有点的度数,则
,矛盾。
Proof:设度数最大的点为 A,则。考虑 G-{A},有 n 个点,且
,由归纳假设知 G-{A}存在 H 回路。由于
,结合抽屉原理可知,一定存在 H 回路上相邻的点,两点都与 A 相连。则将 A 插入到这两点之间,即得到 G 的 H 回路。
10.
设 个人中,任两个人合在一起都认识其余 n-2 个人。证明:这 n 个人可以排成一队,使相邻者都互相认识。
将两人相识视为两点有边。在 2.4.5 中,已经证明,对任意两点 A,B,若 AB 相邻,则. 故只需证,若 AB 不相邻,也有
。
Lemma:若 AB 不相邻,则所有其他点都与 AB 相邻。
反证法。不妨设存在 C 与 A 不相邻,则 BC 合在一起不认识 A,矛盾。
Proof:由于,故除去 AB,至少还有 2 个点。故 AB 至少同时认识两个人,故
。由推论 2.4.1 知,存在 H 回路,即原题有解。
12.
不能。理由如下:
将立方块视为点,立方块相邻则对应点之间有边,再将 8 个角块与中心块连边,得到图 G。原题转化为求 G 的 H 回路。图 G 是二分图(即,可以将点黑白染色,满足同色的点不相邻)。若 G 中有 H 回路,该回路一定是黑白交替地走过全部节点,即回路上黑点与白点数量相同。由于为奇数,故 G 中没有 H 回路。
14.
分支定界法
记原点为 0,四个坐标依次编号 1, 2, 3, 4. 得到权矩阵:
| 0 | 7 | 12 | 17 | 12 |
|---|---|---|---|---|
| 7 | 0 | 9 | 10 | 5 |
| 12 | 9 | 0 | 7 | 6 |
| 17 | 10 | 7 | 0 | 5 |
| 12 | 5 | 6 | 5 | 0 |
1 | d(1)=d[(2, 5), (4, 5), (3, 5), (1, 2), (3, 4)]=30,invalid |
所以最优解为d(24)=36.
便宜法
1 | min w(i,k): |
边权和:42
路径:125341
补充题
1.
凸 n 边形及 n − 3 条在 n 边形内不相交的对角线组成的图形称为一个剖分图.
求证:当且仅当 3|n 时,存在一个剖分图是可以一笔划的图 (即可以从一个顶点出发,经过图中各线段恰一 次,最后回到出发点)
充分性:设,顶点依次为
.连接
,共
条边,形成
个三角形。欧拉回路为:从
开始,先走
个形成的三角形,再沿多边形的边界走回
.
必要性:容易使用归纳法证明:凸 n 边形连接 n-3 条不相交的对角线得到的每个小区域一定是三角形,可以将每个三角形黑白染色,使得相邻的三角形颜色不同。由欧拉回路的性质可知每个点的度数为偶数,因此每个顶点是奇数个三角形的顶点,与多边形有公共边的三角形颜色相同,不妨设为黑色。
对于每个顶点,以它为顶点的黑色三角形数量比白色的多一个。设黑白三角形各有个,则
,所以
.
2.
不存在。我们首先考虑子图:
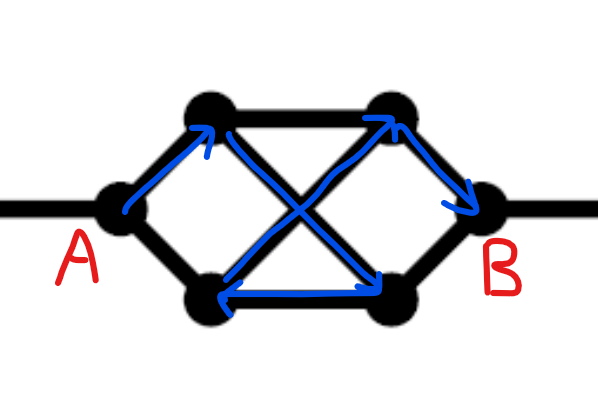
由于 A 和 B 仅能经过一次,因此当路径到达 A 时,必须沿着子图的哈密顿路径到达 B,这样的路径是存在的,如图中蓝色路径。因此,这个子图可以缩为一个点。由此得到新图 G’:

图 G’是二分图(即,可以将点黑白染色,满足同色的点不相邻)。若 G’中有 H 回路,该回路一定是黑白交替地走过全部节点,即回路上黑点与白点数量相同。由于为奇数,故 G’中没有 H 回路。故原图 G 没有 H 回路。