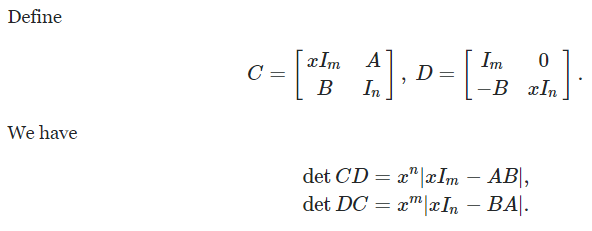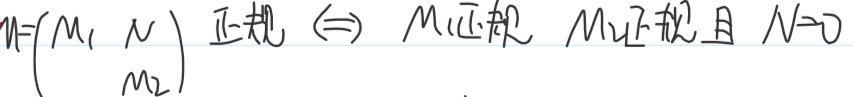线性空间
求两个线性空间的交
借助Row Echelon Form!
先把两组基按列排在一起,然后REF的每一个非主元列给出的就是它的构成!类似于,把右下角再进行一次消元的感觉。
Idea from this.
证明线性空间相等
- 相互包含
- 包含且维数相等
- 包含基
线性变换/矩阵
求广义Jordan型的基
核心思想(来自sympy的代码实现):对于每个特征值,从中选择一个向量,然后生成这个Jordan块对应的基,然后从上述空间中继续选择向量,且和之前选的向量线性无关,直到空。
证明可逆的思路
- 行列式
- Kernel
- RREF
- 相似
证明不可逆的思路
- 在某个子空间不可逆
证明矩阵相似的思路
- 不变因子组相同
正规矩阵的性质
![image-20210519224048226]()
- 正规矩阵A的(共轭)转置是A的多项式(https://math.stackexchange.com/questions/1753539/show-for-a-normal-a-pa-for-some-polynomial-p )
- 正规矩阵的乘积不一定正规。
- A和
共用特征向量,特征值共轭。
是A的多项式(https://math.stackexchange.com/questions/857291/t-is-normal-if-and-only-if-for-every-t-invariant-subspace-its-orthogona#comment1768647_857291 )
- 矩阵
和A^T的属于不同特征值的特征向量正交。
正交相关


不等式相关
- Cauchy
- Frobenius:
![image-20210620144616546]()
二次型相关
矩阵的正负惯性指数和子空间的关系:
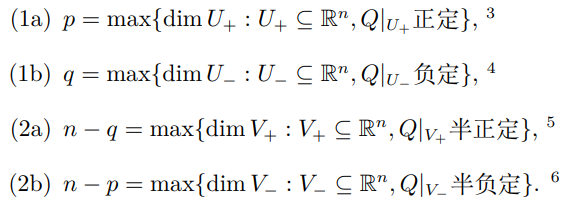




可同时对角化
AB=BA
- A, B实对称。若A还正定,则A可对角化为
作业
wk3 6(2)

整个第6题都值得看看。
wk7 5
利用复数的共轭,和.
扩展:无实平方根。链接

幂零阵的平方根:链接
wk12 4.

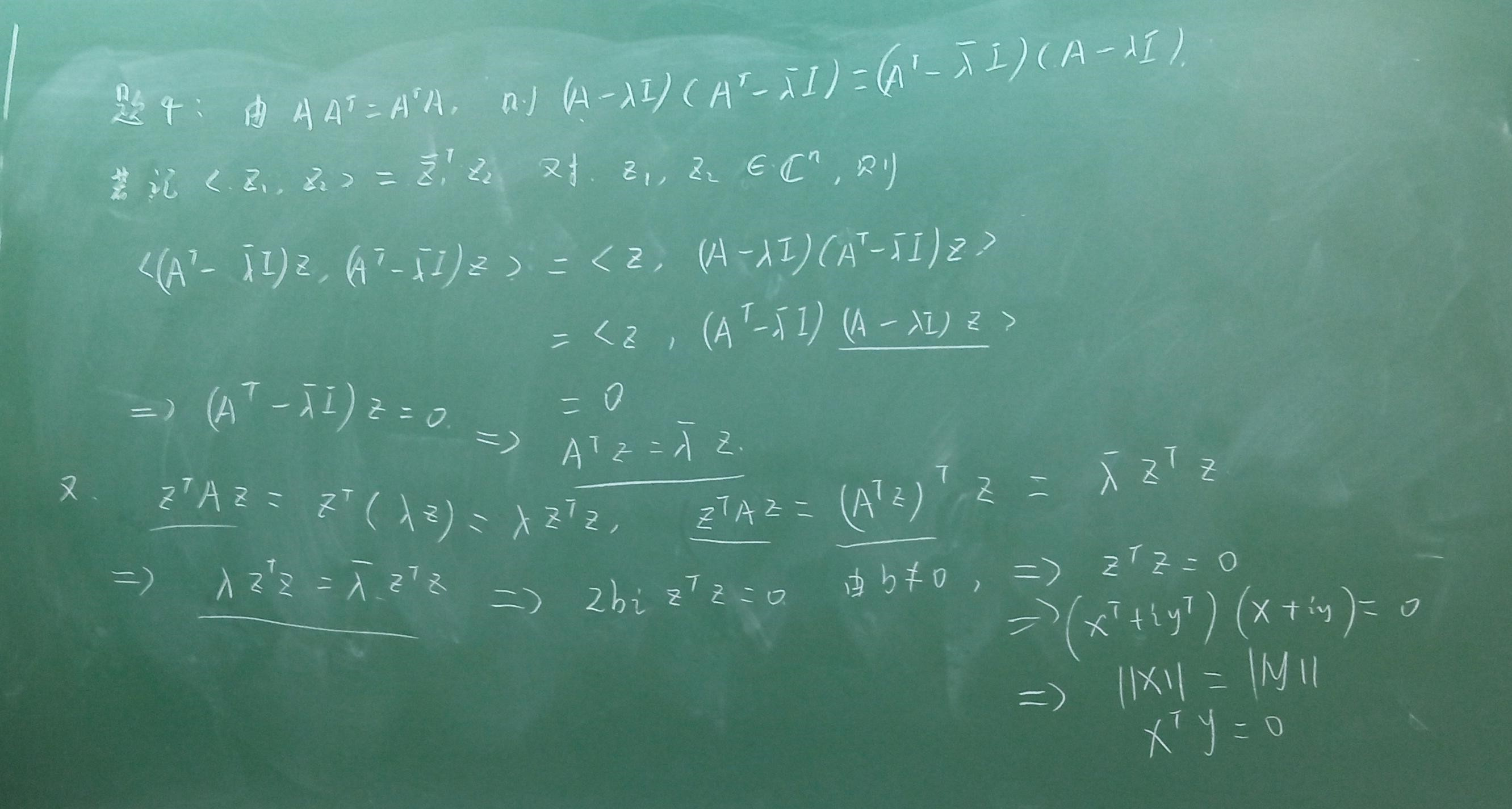
wk13 2.
这个想法很妙,直接考虑把B干掉:

其他

wk8hw 6. 10. 11.
wk10hw 10. 17.
wk11hw 9.
wk12hw 6.
wk15hw 4.
技巧&注意事项
见到复数,想到共轭。
线性空间的维数定理。证明两个空间有交。
伴随矩阵是[代数余子式]的转置!
计算01矩阵的平方根?将矩阵视为某个邻接矩阵的平方,则数字就代表路径条数!
如何使用多项式互素的条件?Bezout定理!
若A,B可交换,则共有一个特征向量。
注意平方和正负的关系。
考虑边界情况,如n=1.
高维内积空间的勾股定理是可用的。
遇到同时出现两个矩阵的情况,先把一个矩阵变成简单的,然后再搞。
取Trace。
谱分解,奇异值分解。