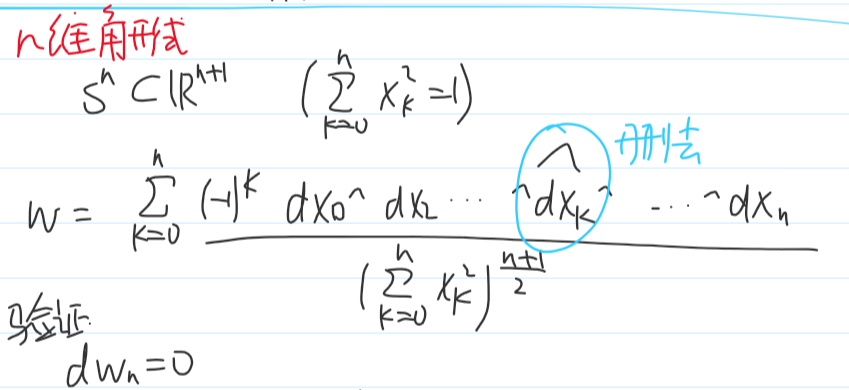多元微分
区域:联通开集
凸区域上的凸函数一定是D上的连续函数。

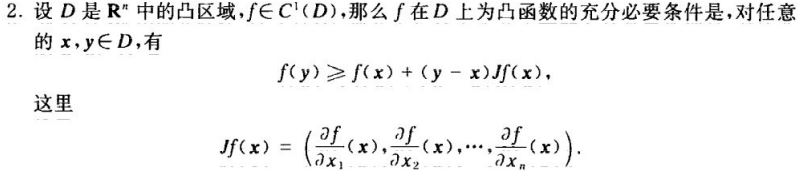
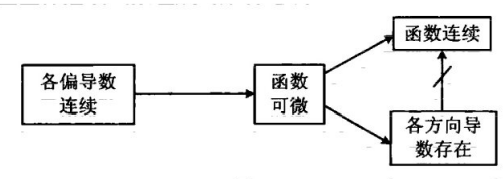
对梯度的理解
梯度是向量场的对偶向量(V的对偶空间:V上的线性映射的集合)。
向量可以被定义为:可以给函数求方向导数。
1-形式就是梯度。

对多元微积分中![]() 的理解
的理解
核心在如何理解余切空间。
函数芽:点任意小的邻域内相等的函数构成的等价类。
余切空间:对函数芽求方向导数。


因此,.
定理们
隐映射定理/隐函数定理:映射
行满秩,则存在
函数
,且
。其中隐函数定理是局限在2维的版本。

逆映射定理/反函数定理:映射
,则存在
且

秩定理:
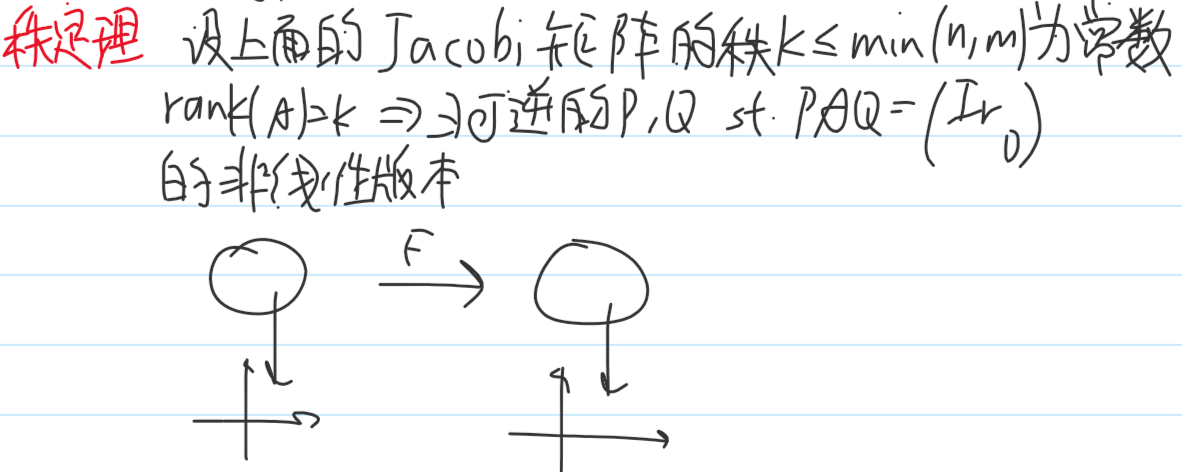
曲线和曲面
光滑曲线:连续可导,且正则(各向导数不同时为0)
零面积集:有限个矩形

B有面积当且仅当B的边界是零面积集。
曲率和挠率
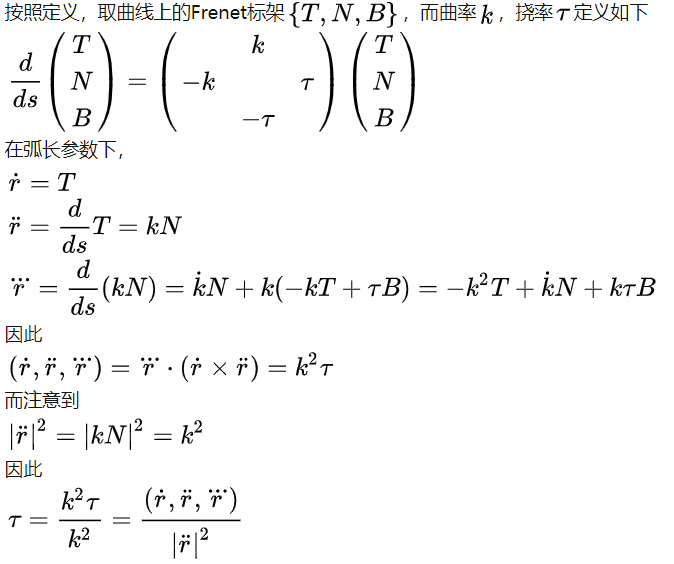
记住:
第一型曲线积分
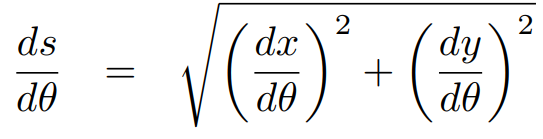
第二型曲面积分

场
div (divergence) 散度,即通量,
rot (rotation) 旋度,即环量,
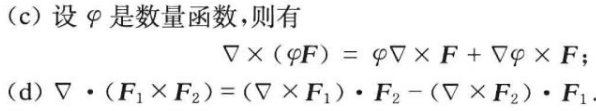
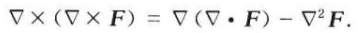
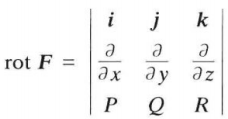
有势场 == 保守场 == 无旋场
旋度场 == 无源场
,则G称为F的向量势,且对于任意连续可微函数
,有
也是F的向量势。
公式们
Green
把封闭曲线积分转为封闭区域的积分。


对于的单/多连通区域和连续函数来说,积分与路径无关 == 恰当微分。
对于的单连通区域和连续函数来说,积分与路径无关 == 恰当微分 ==
。
Gauss
把封闭的曲面积分转为三重积分。
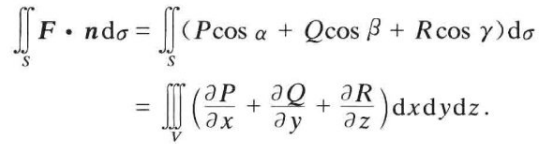
Stokes
把曲面的边界积分转为曲面积分。


其中是
的单位切向量。
高维Stokes:
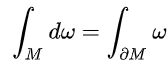
微积分
几个积分的式子:
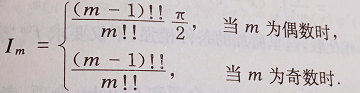
极坐标换元的Jacobi行列式:
二维:
三维:,其中
三角函数

反三角函数

双曲三角函数
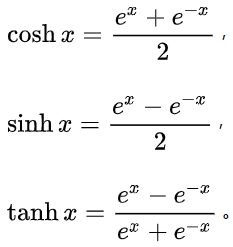
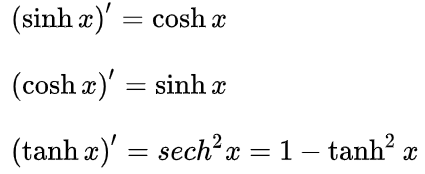
https://zhuanlan.zhihu.com/p/20042215
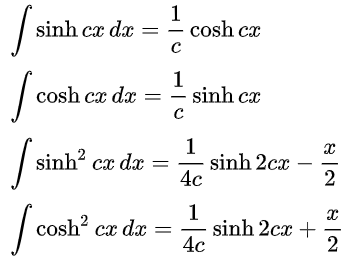
线性代数
正交矩阵
注意到 ,也就是说矩阵的行(或列)向量之间点积等于0(向量正交),行(或列)向量与自身的点积等于1(单位向量),所以正交矩阵又有另一种定义:由行之间两两正交、列之间两两正交的单位向量组成的方阵。
技巧&注意事项
证明闭集:
- 补集是开集
- 对取极限封闭
连续映射:开集的原象是开集
子空间拓扑
注意球坐标换元后变量的范围:。高维情况类似,只有最后一个角(也就是出现全
的)的范围是
证明某个区间都满足某个性质的方法:设
利用连通性、开集来证明
多元微积分泰勒公式
拟微分平均值定理
化为一元
很多时候直观是错的,或者说直观只在一维成立。但是可以用直观进行验证,例如简单的等式。
用对称性简化运算!
配方
聚点定理+开覆盖证明和闭集有关的定理。
似乎周坚的考试题有一部分出自《组合优化》
让我预言一下明天考什么:
格林公式,等周问题,麦克斯韦方程组,角形式
周坚习题课上埋的伏笔:
高斯积分,傅里叶分析,椭圆积分