出发之前，打算留一台服务器在校内。打算重新利用下旧手机，是曾经的中端机皇Redmi Note 4X，当初怂恿老妈买就是因为酷安上很多人都在夸，而且包多教程多。现在终于有时间搞一搞了。
上次鼓捣什么TWRP，Magisk还是初中的时候吧，上了高中以后就佛系了，手机都不Root了，养老。
这次的目标是SSH+VNC+Docker+Proxy。
先解锁Bootloader，然后打算刷TWRP，结果看到什么dm-verify不知所讲，遂打算先装Magisk。下载原版ROM，修补boot.img，fastboot刷入。
1 | adb shell settings put global captive_portal_fallback_url http://g.cn/generate_204 |
接着再搞定：Clash TUN、sshd、crond。
最后实际上一次都没用上…
写在前面：本文是作为概率论与数理统计的课程论文。
想必大家在学习概率论的时候，都听过这样一个故事：一只猴子在打字机上随机敲击键盘，无限期地敲下去，最终会打出一部莎士比亚的作品。这个故事的出处[1]有许多说法，最初提出这个故事的人也不一定是英国人（那么提到的作品也大概不是莎士比亚的），这里不做细究。但是这个故事的意义却是显而易见的：在无限的时间里，一切都有可能发生。
这种一定发生的事情是多么的无聊。按照清华的传统，我们不妨把它变成一个比赛，排出一二三来。对猴子（学生）排序这件事，听起来有些恐怖。我们还是比一比哪部作品更容易被猴子写出来吧。我虽然读过莎翁的几篇著作，但是它们在我的榆木脑袋里并没有留下太多印象，而且不同作品的字数也不一样，显然不太公平。我们不妨比较一些字数相近的作品，中国古代的五言绝句就是一个很好的选择。我拍脑袋想到了《静夜思》和《八阵图》这两首诗，于是，我们的问题就是：一只猴子随机敲击键盘，更容易写出《静夜思》还是《八阵图》？
看到这里，很自然的一个想法是，两首诗长度相同，那么出现的概率自然也相同了。其实，问题没有这么简单。为了看清楚这一点，我们需要简化问题。键盘上的按键太多了，我们干脆让猴子抛硬币吧，这样我们得到的就是无限长的01序列（0代表正，1代表反），每个位置的结果独立，且0和1出现的概率相等。《静夜思》和《八阵图》这两首诗，我们暂且用011（正反反）和110（反反正）来表示，以便于猴子写出来。那么，这两个序列，哪一个先出现的概率高？
事实上，011首先出现的概率高达75%！虽然011和110的长度相同，出现的频率也是相同的，但是它们之间存在竞争（太可怕了）！011的第一个0出现的时候，110已经输了，因为它的第一个1还没有出现。在110的前缀11出现时，011就会取得胜利。因此，二者的胜率是3:1。
校内服务器需要魔法来运行一些程序，之前我的做法是在公网上开一个带认证的SOCKS DL（校内互联肯定不会过墙）。可是前几天USB网卡挂了，就只好另寻出路。
经过搜索，发现了ssh -D这个方便的DL，它的原意是动态端口转发。执行 ssh -D8080 remote_server 就会在本机的8080端口开一个SOCKS DL，出口为remote_server。那么我们在校内服务器ssh到VPS即可。
测了下速，可以跑满。延迟的话，无负载时延迟是正常延迟，但是在高负载时延迟巨大，原因应该是SSH加密解密的开销。
进一步搜索发现了 pproxy 这个Python库，可以把各种不同的协议互相转换。
至此，问题解决。
五一去看了若干部电影，有笑有泪，五月最佳（
这是我看的第一部日本动画电影，看完之后我很想补完新海诚的前两部作品。之前看过很多国产的，大鱼海棠、哪吒、大圣、喜羊羊。给我的感觉，总觉得差点。
我是很喜欢这部电影的，首先因为它的主题。导演在一部电影里提到了日本的自然灾害（地震）、单亲家庭、乡村的消亡，以铃芽的成长作为线索穿起来。过程中让我了解了许多日本的传说故事（往世、蚓厄），寄托在一扇小小的往门后。公路电影的特点又让我对日本的风土人情有很多的了解，并且挺想去看看的？也许是第一次看日本动画电影，所以才有这么多新鲜感吧。
影片的主要缺点是主角的动机。我不是很能体会到小女孩为什么如此想救哥哥，连他爷爷都没觉得心疼。还有一些情节是多余的，导演要么表达清楚，要么显得拖沓。
我觉得大臣挺可爱的，是谁敢假定要石的角色的？
（庆幸）这部没去电影院看。
前几天发现了通过53端口实现免认证热点上网的方式，在你清不堪的校园网里一试，果然没有防备，于是美滋滋的搭建了一个代理，以后可以免费上网了~
如标题所写，此处是“白嫖校园网基础设施”，实现免登录上网、无限流量上网，但是并不能白嫖校园网，即无法获得教育网的IP地址。同样，公网的服务器也需要购买。
其实道理挺简单的，网关（交换机）都默认放行 DHCP 和 DNS 报文，也就是 UDP53 与 UDP67/68。有些网关（你清网关）甚至不会对报文进行检查，这也就意味着任何形式的数据包都可以顺畅通过。
所以方法就很简单了，随便找个UDP协议的软件，监听53端口就行。可以用原文里提到的SoftEther VPN，但是都3202年了，meet the WireGuard.
其实挺简单的，安装服务端和客户端，写一份配置文件，然后wg-quick up wg0即可。为了支持IPv6我还鼓捣了一会儿，这里提供一下我的配置文件：
1 | [Interface] |
客户端：
一切的一切源自于2021年的Cloudcone促销，入手了一台1核+1G+40G+2TB/mo，用作代理。惊讶于超级稳定，毫无波澜地扛过上半年和下半年的大考。后来又发现了更多可以在VPS上部署的东西，于是…收集癖。
经常陷入死循环：VPS限制了，找点事情干；找到了，VPS不够用了，再买点。
（不全）
20220124：受宝硕的博客启发，用Cloudflare Warp给俺的VPS加个IPv6隧道。五分钟后决定鸽了
20220130：发现俺的域名证书快到期了，自动续期失败了。但是俺已经忘了当时怎么配置的了。完蛋，只能使用休克疗法了。
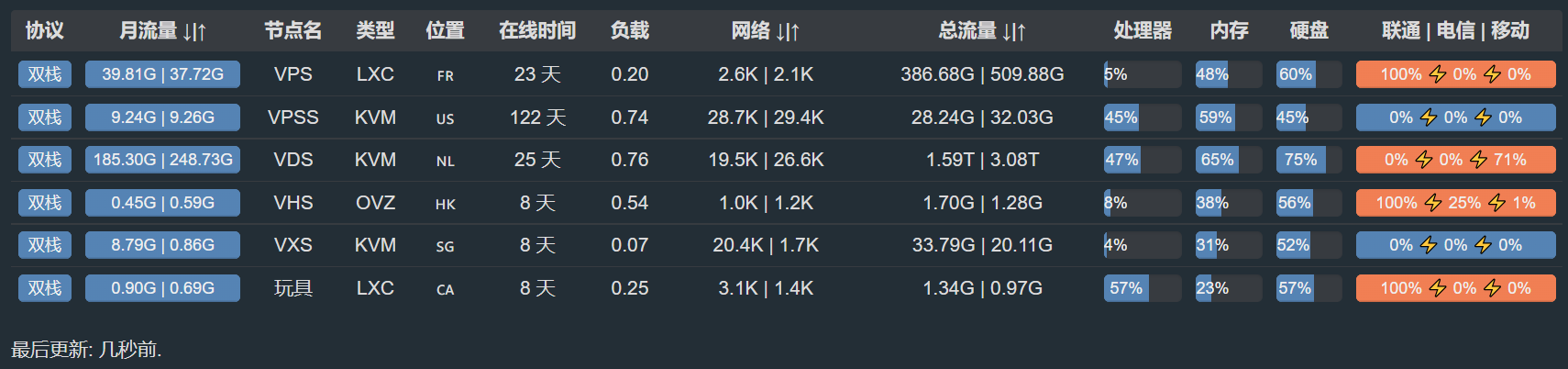
20221207：现在的样子（预购了一台日本机）：
